神经工程框架技术综述
神经工程框架(NEF)是一种通用的方法,可以建立大规模的、生物学上合理的认知神经模型。
动机
起初,对于一些人来说,我们想要创建生物学上合理的认知模型似乎很奇怪。为什么要这么麻烦?为什么要用额外计算开销使建模神经元更加逼真?当我们很难创建能够产生现实认知行为的模型时,为什么我们要对我们的模型施加这种额外的约束?
对我们来说,主要有两个原因。首先,使用逼真的神经元可以让我们更好地评估我们的理论。如果我们想了解大脑是如何工作的,那么我们的模型不仅应该产生正确的行为,而且产生方式应该也与真实大脑相同。也就是说,我们应该看到类似的放电模式和神经连接。应该看到神经退化、病变、脑深部刺激,甚至各种药物治疗的等价效果。应该看到神经元的生物物理特性所引起的相同时间效应。事实上,当我们使用 NEF 实现了一个产生系统,并将模型限制为只具有大脑相关区域中存在的各种神经元类型的特性时,它在没有参数拟合的情况下产生了典型的 50 毫秒认知周期时间。此外,它产生了一个新的预测,即某些类型的产生需要约 40 毫秒,而另一些类型的产生则需要约 70 毫秒,这与一些无法解释的行为数据非常吻合。换句话说,逼真的神经元使我们能够创建新类型的预测,并使我们能够基于生物学设置模型参数。
如果说第一个原因可以让你更好地评估模型,那么第二个原因是使用逼真的神经元促使产生新类型的算法。当使用 NEF 时,无论指定什么算法,都无法得到准确的实验。相反,如果神经元是近似这个算法,那么这个近似的准确性不仅取决于神经特性,还取决于正在计算的函数。也就是说,NEF 迫使你使用神经元可用的基本运算,而不是在你的模型中使用任何计算。这使我们能够有力断言无法在人脑中实现的算法类别(考虑到时间、鲁棒性和所涉及神经元数量的限制)。特别是,找到一种可行的方法来实现类似符号的认知推理,包括符号树操作,使我们走向了一个相对未经探索的算法领域。正如我们下面将要讨论的,这些替代方法对归纳和模式完善任务特别有用,因为这些任务很难用经典符号结构来解释。
当然,一旦识别出这些新型算法,就可以在不使用逼真神经元的情况下对其进行探索。事实上,我们的软件包 Nengo 允许任意控制神经元的使用,无论是针对整个模型还是仅针对特定部分,即使在模拟运行时也是如此。然而,我们发现在一些情况下,神经实现中产生的近似值实际上改善了模型(就其与人类数据的匹配而言)。换句话说,即使一个理论的标准数学实现与经验结果不匹配,该理论的 NEF 模型也可能做得更好。
表达
NEF 使用Distributed Representation。特别是在一组神经元的活动和所代表的价值之间做出了鲜明的区分。所表示的值通常被认为是向量 $\mathbf{x}$。例如,您可以使用 100 个神经元来表示二维向量。不同的向量值对应于这些神经元的不同活动模式。
为了在 $\mathbf{x}$ 和神经元活动 $a$ 之间进行映射,每个神经元 $i$ 都有一个编码向量 $\mathbf{e}_i$。这可以被认为是该神经元的首选方向向量:该神经元最强地激发时的向量。这符合为神经元建立调谐曲线的一般神经科学方法,其中神经元的活动在某些刺激或条件下达到峰值。尤其 NEF 强烈要求神经元的输入电流是所表示值的线性函数。如果 $G$ 是非线性神经元,$\alpha_i$ 是增益参数,$b_i$ 是神经元的恒定背景偏置电流,那么我们可以计算给定 $\mathbf{x}$ 的神经活动,如下所示:
$$a_i = G{({\alpha_i}{\mathbf{e}_i}\cdot{\mathbf{x}} + {b_i})} {\tag{1}}$$
重要的是,函数 $G$ 可以是任何神经模型,包括简单的基于速率的 Sigmoid 神经元、Spiking Leaky-Integration-and-Fire 神经元,或更复杂的生物学细节模型。唯一的要求是在输入电流和神经元活动之间有一些映射,这可能包括复杂的尖峰行为。
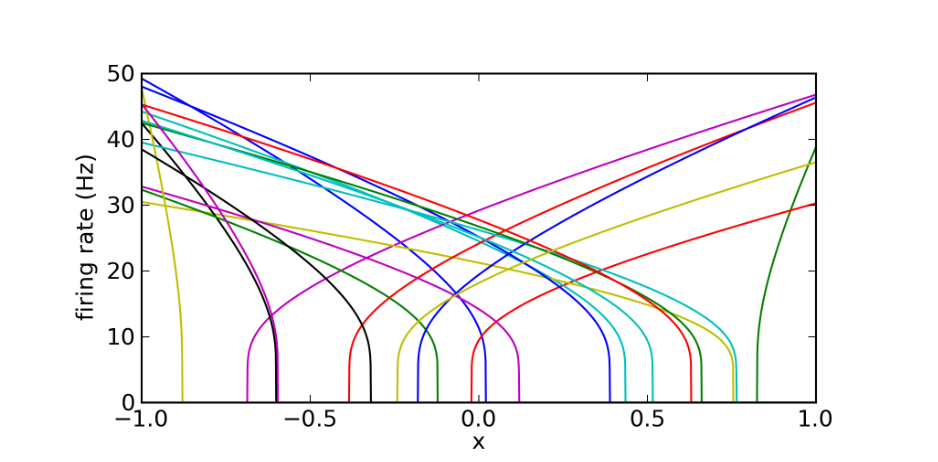
在标准的连接主义模型中,每个神经元对输入的一个不同分量做出反应。我们可以将其视为方程 1 的一种特殊情况,其中所有 $\mathbf{e}_i$ 值都沿着标准基向量对齐(对于二维情况,为[1,0]和[0,1])。如果一个非尖峰神经元实际上是一个尖峰神经元池,那么这就像具有相同的 $\mathbf{e}_i$、 $\alpha_i$ 和 $b_i$ 值。然而,真实的神经元具有广泛变化的值(见图 1)。允许这些值发生巨大变化会大大提高这些神经元的计算能力,正是下一节所讨论的。
虽然方程 1 允许我们将向量 $\mathbf{x}$ 转换为神经活动 $a_i$,但反过来也很重要。也就是说,给定一些神经活动 $a_i$,$\mathbf{x}$ 代表什么值?其中最简单的方法是找到一个线性解码器 $\mathbf{d}_i$。这是一组权重,负责将活动映射回 $\mathbf{x}$ 的估计值,如下所示:
$$\hat{\mathbf{x}} = \sum{a_i}{\mathbf{d}_i} {\tag{2}}$$
这句话的意思是:找到这组解码权重 $\mathbf{d}_i$ 是一个最小二乘问题,因为我们想找到最小化 $\mathbf{x}$ 和其估计值之间差异的权重集。这是一个标准的代数问题,可以通过以下方式解决,其中总和是在可能的 $\mathbf{x}$ 值的随机抽样上进行的。
$$\mathbf{d}=\Gamma^{-1} \Upsilon \quad \Gamma_{i j}=\sum_{\mathbf{x}} a_{i} a_{j} \quad \Upsilon_{j}=\sum_{\mathbf{x}} a_{j} \mathbf{x} {\tag{3}}$$
有了这个解码器,你就可以确定一组神经元代表某种值的准确程度,并对该组神经元的尖峰活动提供更高层次的解释。更重要的是,这些解码器还允许您直接求解神经连接权重,该权重将计算一些所需的变换,如下所示。
计算
到目前为止,我们已经指定了如何将向量编码到神经元群体的分散活动中,以及如何将这种活动解释回向量。然而,要做任何有用的事情,神经元都需要连接在一起。考虑一个简单的例子,你有两个神经群体(A 和 B),你想把信息从一个群体传递到下一个群体。也就是说,如果你将 A 设置为表示值 0.2,那么 A 和 B 之间的突触连接应该会导致 B 中的活动也表示值 0.2。换句话说,您希望 A 和 B 之间的连接计算函数
$f(\mathbf{x})=\mathbf{x}$。
重要的是,你不能简单地将 A 中的第一个神经元连接到 B 中的第一个神经元,以此类推。这两组中不仅可能有不同数量的神经元,具有不同的 $\alpha_i$ 和 $b_i$ 值,而且非线性神经元 $G$ 使这种天真的方法非常不准确。
为了创建一个准确并且稳固的连接,首先假定我们拥有一个完美理想的线性神经元中间组,并且我们能将他们中的每一个维度表示出来。我们会注意到,由于方程 2,$\mathbf{d}$是在给定 A 的活动中计算 x 所需要的一组连接权重。此外,使用组 B($\mathbf{e}_j$)的编码器值作为 $\mathbf{x}$ 表示的连接权重正是计算方程 1 中点积所需要的,这反过来可以用 B 来表示 $\mathbf{x}$。这个过程会在图 2a 中展示。
当然,真正的大脑没有这些理想化的中间神经元。然而,这是完全不需要的。你可以删除他们并使用通过将两组权重相乘所得的连接权重直接连接 A 和 B(如图 2b)。也就是说,将信息从 A 传递到 B 的最佳权重可以简化为 $\omega_{ij}=\mathbf{d}_{i}\cdot{\mathbf{e}_j}$。