二分法
二分法的基础是在单调序列或单调函数中进行查找。
当问题答案具有单调性时,可通过二分把求解过程转化为判定过程。同时可以扩展到三分法去解决单峰函数的极值问题等……
二分模板
模板以单调递增序列为例
nums = list(map(int, input().split()))
n = len(nums)
sorted_nums = nums.sort() # nums 为单调递增序列
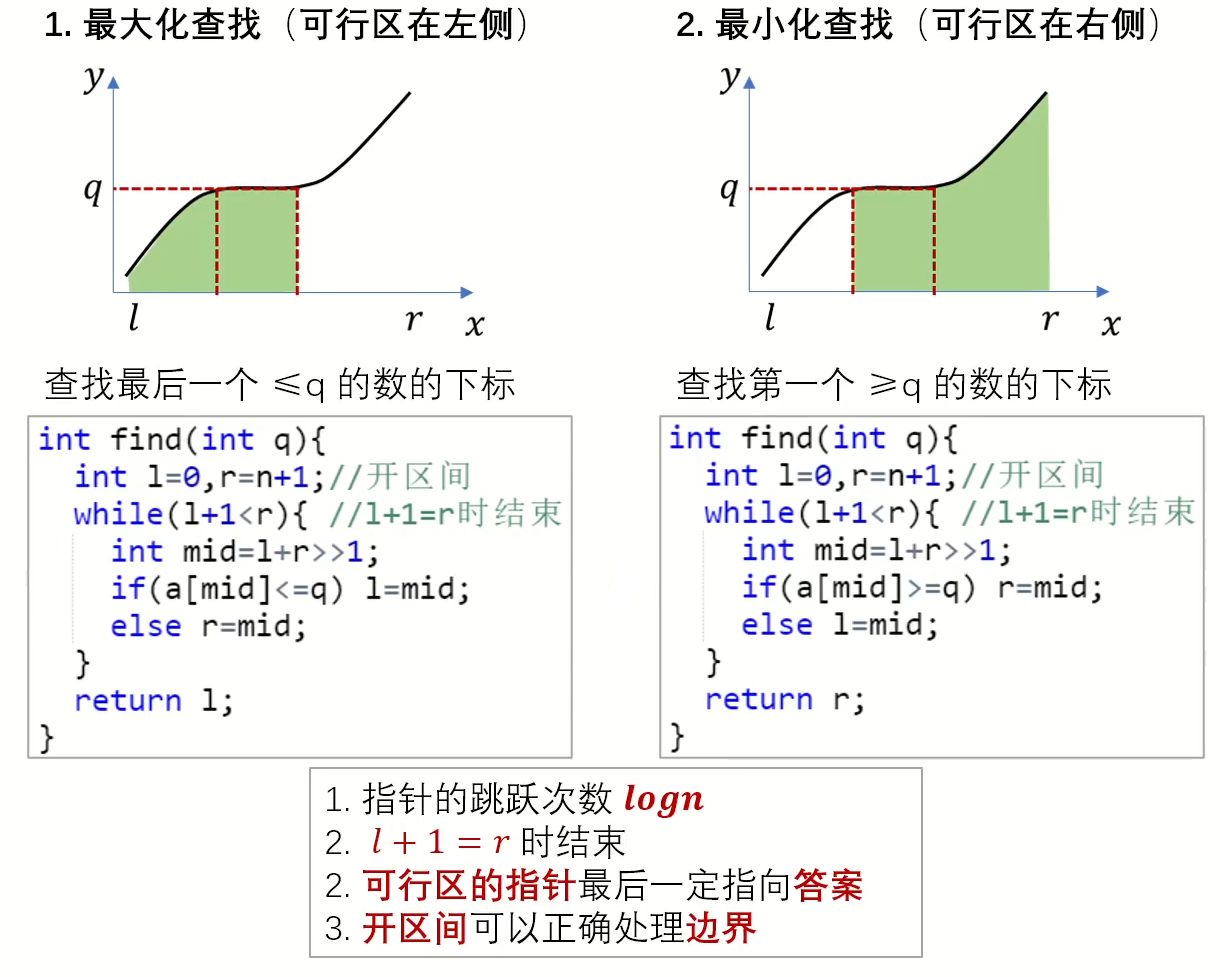
查找最后一个<=x 的数的下标(最大化查找)
def search(x):
l, r = 0, n + 1 # 开区间
while l + 1 < r: # l + 1 == r 时结束循环 保证l、r可行域不重叠
mid = (l + r) // 2
if nums[mid] <= x:
l = mid
else:
r = mid
return l
查找第一个>=x 的数的下标(最小化查找)
def search(x):
l, r = 0, n + 1 # 开区间
while l + 1 < r: # l + 1 == r 时结束循环 保证l、r可行域不重叠
mid = (l + r) // 2
if x <= nums[mid]:
r = mid
else:
l = mid
return r
整数二分
可以理解 l + 1 < r 的 1 为整数间隔,保证每个数不重不漏。
例题 洛谷 P2249 查找
Description
输入 n 个不超过 10^9 的单调不减的(就是后面的数字不小于前面的数字)非负整数 a1, a2, ……, an,然后进行 m 次询问。
对于每次询问,给出一个整数 q,要求输出这个数字在序列中第一次出现的编号,如果没有找到的话输出 −1。
Input
第一行 2 个整数 n 和 m,表示数字个数和询问次数。
第二行 n 个整数,表示这些待查询的数字。
第三行 m 个整数,表示询问这些数字的编号,从 1 开始编号。
Output
输出一行,m 个整数,以空格隔开,表示答案。
Sample Input
11 3
1 3 3 3 5 7 9 11 13 15 15
1 3 6
Sample Output
1 2 -1
Range
$1\le n \le 10^6$,
$0\le a_i$,
$q\le 10^9$,
$1\le m \le 10^5$,
def search(x):
l, r = 0, n + 1
while l + 1 < r:
mid = (l + r) // 2
if nums[mid] >= x:
r = mid
elif nums[mid] < x:
l = mid
return r if nums[r] == x else -1
n, m = map(int, input().split())
nums = [0] + list(map(int, input().split())) + [0]
query = list(map(int, input().split()))
for i in range(len(query)):
print(search(query[i]), end=" ")
浮点数二分
将模板中的+1 间隔改为一个足够小的数字 eps,具体以题目要求为准,同时将判断条件改为符合题意的 check 函数。
当无法确定精度或难以表示时,可以通过固定循环次数来查找。
例题 P1024 一元三次方程求解
Description
有形如: $ax^{3}+b x^{2}+c x+d=0$ 这样的一个一元三次方程。给出该方程中各项的系数 (a, b, c, d 均为 实数),并约定该方程存在三个不同实根(根的范围在 -100 至 100 之间),且根与根之差的绝对值 $\geq 1$ 。要求由小到大依次在同一行输出这三个实根(根与根之间留有空格), 并精确到小数点后 2 位。
提示:记方程 $f(x)=0$, 若存在 2 个数 $x_{1}$和 $x_{2}$, 且 $x_{1}<x_{2}$, $f\left(x*{1}\right) \times f\left(x*{2}\right)<0$ , 则在 $\left(x*{1}, x*{2}\right)$ 之间一定有一个根。
Input
一行, 4 个实数 a, b, c, d 。
Output
一行, 3 个实根, 从小到大输出,并精确到小数点后 2 位。
Sample Input
1 -5 -4 20
Sample Output
-2.00 2.00 5.00
def fun(x):
return a * x ** 3 + b * x ** 2 + c * x + d
def find(l, r):
while l + 1e-5 < r:
mid = (l + r) // 2
if fun(mid) * fun(r) < 0:
l = mid
else:
r = mid
return l
a, b, c, d = map(int, input().split())
for i in range(-100, 101):
y1, y2 = fun(i), fun(i + 1)
if y1 == 0:
print(f"{i:0.2f}", end=" ")
if y1 * y2 < 0:
print(f"{find(i, i + 1):0.2f}", end=" ")
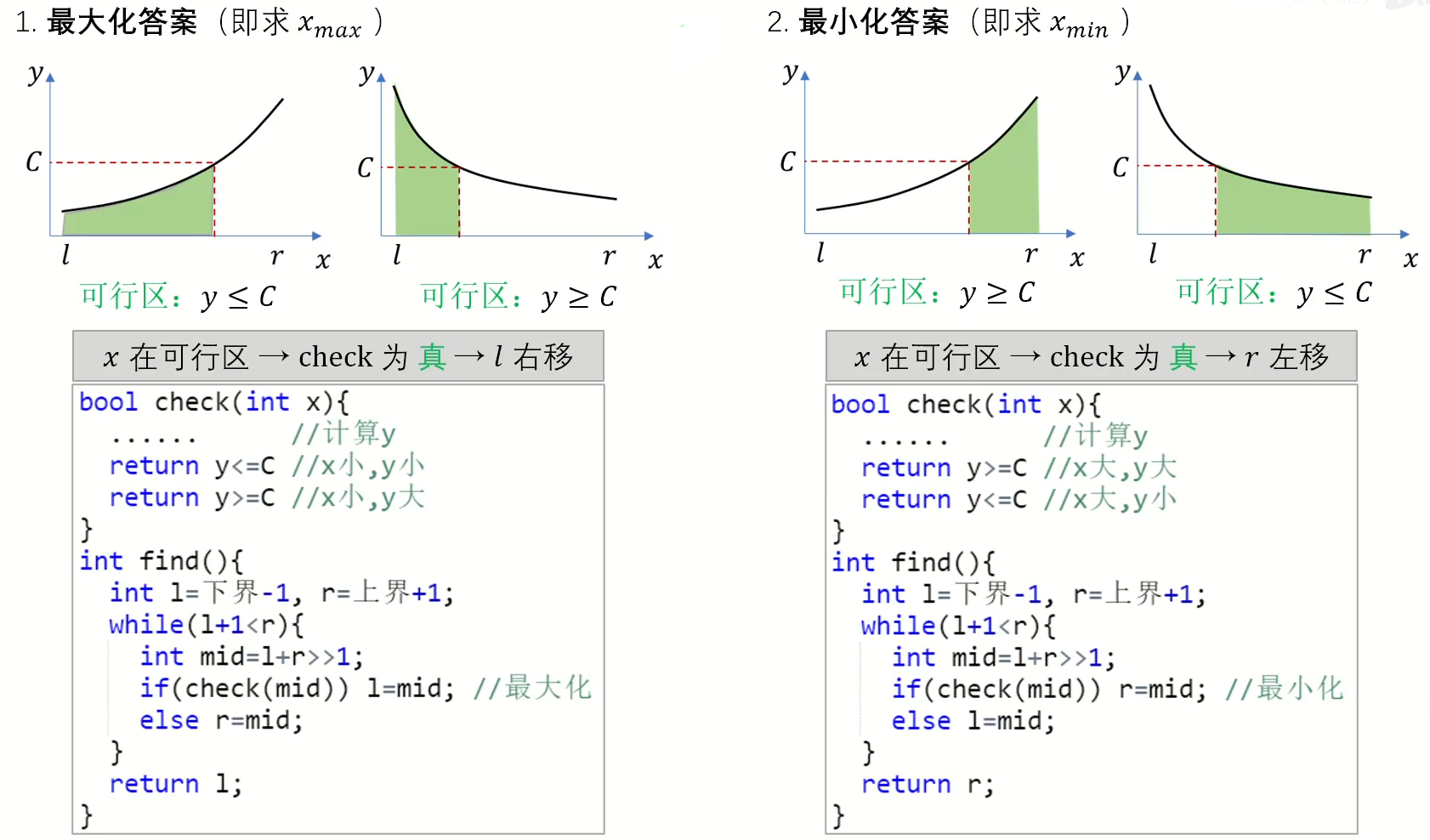
答案二分转换判定
当拥有判定算法时,可通过枚举解空间来求出答案。
当解空间具有单调性时,可以使用二分查找代替枚举。
通常为最优化问题,并且原问题无法直接求解,可以考虑转换为判定问题。
二分答案的结果通常为模拟过程:
- 计数型
- 求和型
- 是否型
并根据图像单调性确定二分方法。
二分答案的本质是建立一个定义域为解空间,值域为0/1的单调分段函数,在这个函数上通过二分查找分界点。
例题 洛谷 P2440 木材加工
Description
木材厂有 n 根原木, 现在想把这些木头切割成 k 段长度均为 l 的小段木头(木头有可能有剩余)。 当然, 我们希望得到的小段木头越长越好, 请求出 l 的最大值。
木头长度的单位是 $\mathrm{cm}$, 原木的长度都是正整数, 我们要求切割得到的小段木头的长度也是正整数。 例如有两根原木长度分别为 11 和 21 , 要求切割成等长的 6 段, 很明显能切割出来的小段木头长度最长为 5 。
Input
第一行是两个正整数 n, k , 分别表示原木的数量, 需要得到的小段的数量。
接下来 n 行, 每行一个正整数 $L_{i}$, 表示一根原木的长度。
Output
仅一行, 即 l 的最大值。
如果连 1 $\mathrm{~cm}$ 长的小段都切不出来, 输出 0 。
Sample Input
3 7
232
124
456
Sample Output
114
"""
段数y时关于段长x的减函数
通常判定关系可以由提问直接得出,若给出条件无单调性,需寻找另外条件作为判定关系。
"""
def check(x):
global ans
y = 0
for i in range(1, n + 1):
y += L[i] // x
if y >= k:
ans = x
return True
else:
return
n, k = map(int, input().split())
L = [0] * (n + 1)
for i in range(1, n + 1):
L[i] = int(input())
ans = 0
l, r = 0, max(L) + 1
while l + 1 < r:
mid = (l + r) // 2
if check(mid):
l = mid
else:
r = mid
print(ans)
其他例题
洛谷 P2678 跳石头
洛谷 P1314 聪明的质检员
洛谷 P1083 借教室
洛谷 P1902 刺杀大师
AcWing 102 最佳牛围栏
AcWing 103 特殊排序